流体シミュレーションを実装してみたいその４（最適化編）

はじめに

こんにちは。株式会社スパーククリエイティブCTOの広本です。
普段は SPARK GEARの開発をしたり、UEでエンジンの改造をしたり、Unityでレンダラーや揺れもの物理を作ったりしています。

第3回までの内容で爆発のシミュレーションを作ることは出来ました、しかしこれら実装できたとしても、高解像度で実行すると、FPSは一桁に落ち込みます。
流体シミュレーションは、計算量とメモリ帯域の塊です。

今回は、リアルタイム動作を実現するための最適化に関して解説します。

はじめに
1. データ構造の最適化
- バッファ精度の半減化 (FP32 → FP16)
- 遮蔽マップの低解像度化
2. カーネルフュージョン
3. 圧力ソルバの最適化
まとめ

1. データ構造の最適化

GPUプロファイリングを行うと、流体シミュレーションの多くの工程が Memory Boundであることが分かります。
ALUは暇をしているのに、VRAMからのデータ転送が間に合っていない状態です。

バッファ精度の半減化 (FP32 → FP16)

そこで、物理的に許容できる範囲でバッファの精度を float (32bit) から half (16bit) に落とします。

速度場・密度場: R16G16B16A16_FLOAT  
圧力場: R16_FLOAT

これにより以下のメリットが生まれます。

メモリ帯域の節約: 読み書きするデータ量が単純に半分になります。帯域律速のカーネルでは、これだけで実行速度がほぼ2倍になります。  
VRAM容量の節約: 大規模グリッドを確保する際のリソース不足を防げます。  
ALUスループット向上: 近年のGPUアーキテクチャでは、FP16演算をFP32の2倍のレートで実行できるものが多いです。


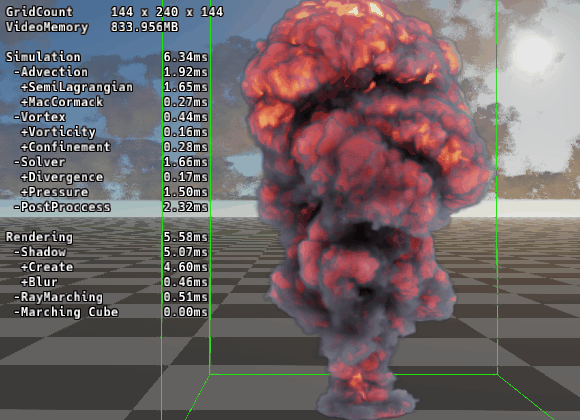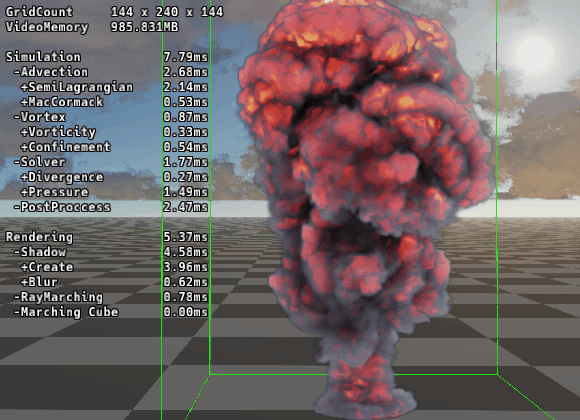▲ FP16	▲ FP32

見た目にはさほど違いは出ませんが明らかに処理負荷は減っています。
ただし、圧力計算の累積誤差が気になる場合は、圧力場のみFP32を残すといったハイブリッド構成も有効です。

遮蔽マップの低解像度化

第1回で紹介した「セルフシャドウ用の遮蔽マップ」ですが、これは生成後にガウスブラーをかけてソフトシャドウ化しています。

ここに最適化のヒントがあります。
「どうせ後でボカすなら、最初から高解像度で作る必要はない」のです。

メインの流体グリッド: [256]  
遮蔽マップ: [128] （体積比で1/8）

解像度を半分にするだけで、遮蔽計算（レイマーチング）の計算コストは 1/8 に激減します。
描画時にリニアサンプリングで読み出せば、低解像度感は全く気になりません。
これは、画質を維持しつつ負荷を劇的に下げる最適化です。


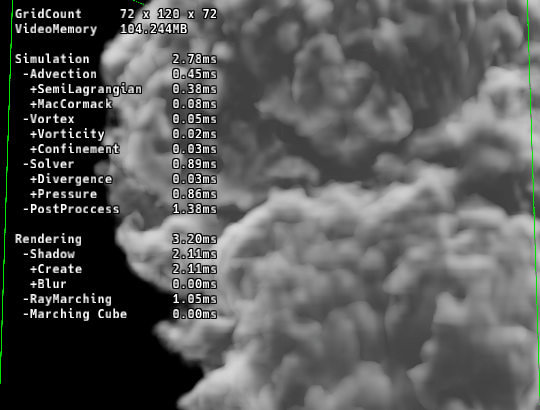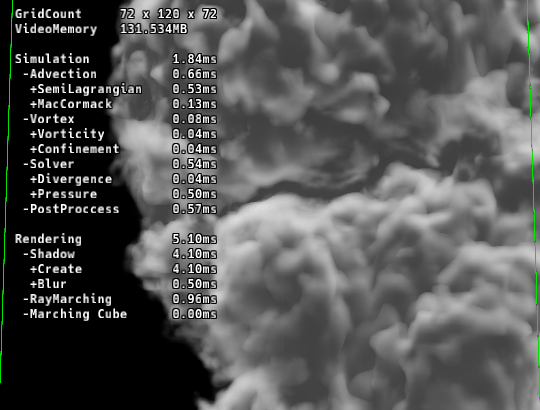▲ 低解像度	▲ 高解像度

こちらも見た目にはほとんど差はないですが、Shadowの生成処理が明らかに軽くなっています。

2. カーネル フュージョン

流体シミュレーションの教科書的な実装では、工程ごとにCompute Shader（カーネル）を分けがちです。

Advection.compute (Read -> Write)  
AddForce.compute (Read -> Write)  
Vorticity.compute (Read -> Write)  

...

しかし、これでは毎回VRAMへの読み書きが発生し、メモリ帯域を浪費します。
そこで、依存関係のない複数の処理を1つのシェーダーにまとめる（Kernel Fusion）ことで、オンチップメモリ（レジスタやL1/L2キャッシュ）上で計算を完結させます。

// 統合されたカーネルのイメージ
[numthreads(8, 8, 8)]
void FusedAdvectForce(uint3 id : SV_DispatchThreadID)
{
    // 1. 移流計算
    float4 quantity = Advect(...);
    
    // 2. 外力計算 (VRAMに書き戻さず、レジスタ上の値をそのまま使う)
    quantity += ExternalForce(...);
    
    // 3. 最後に1回だけ書き込む
    _ResultTex[id] = quantity;
}

これにより、Global Memoryへのアクセス回数を減らし、実効パフォーマンスを向上させることができます。


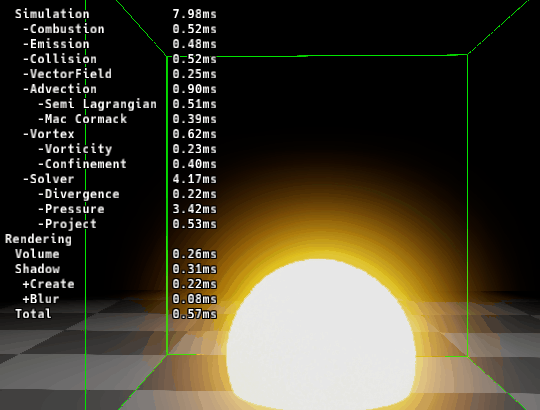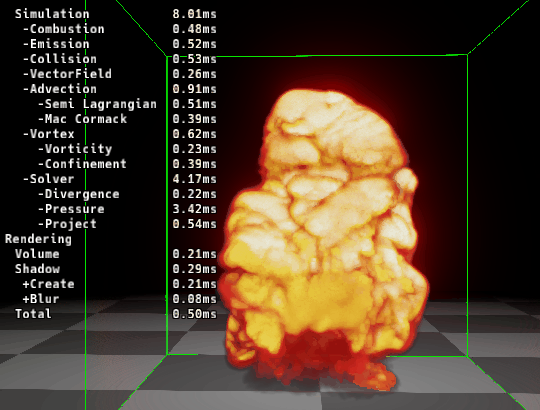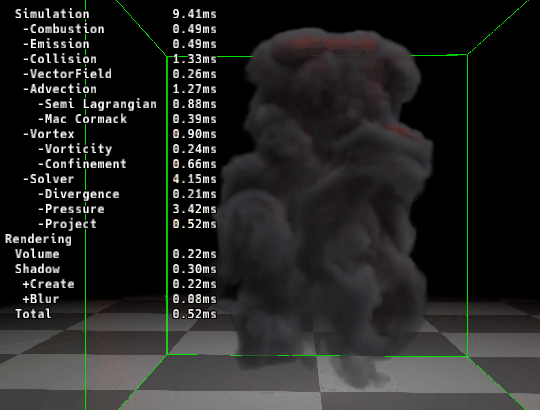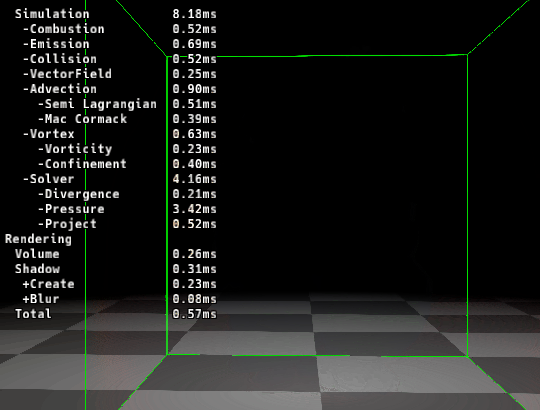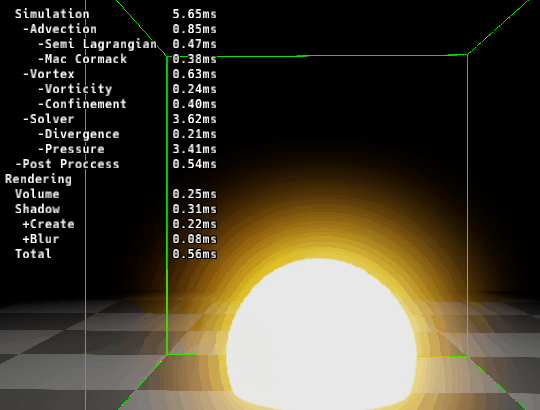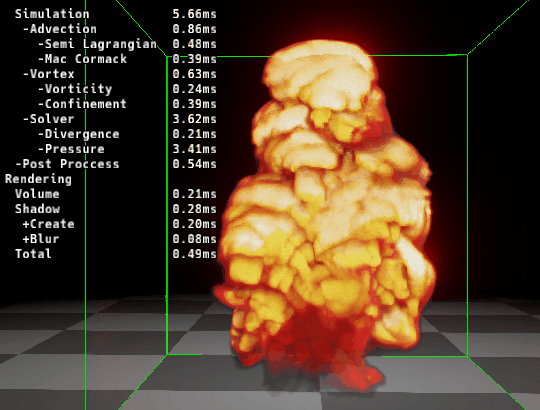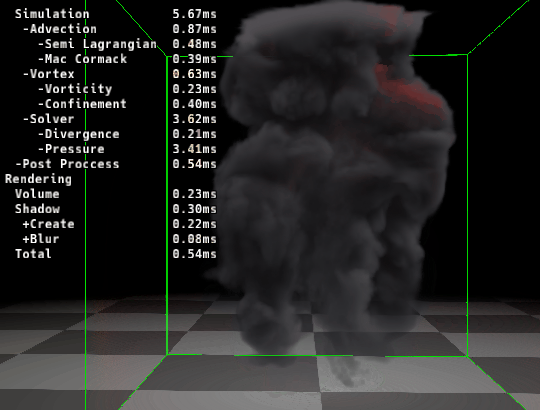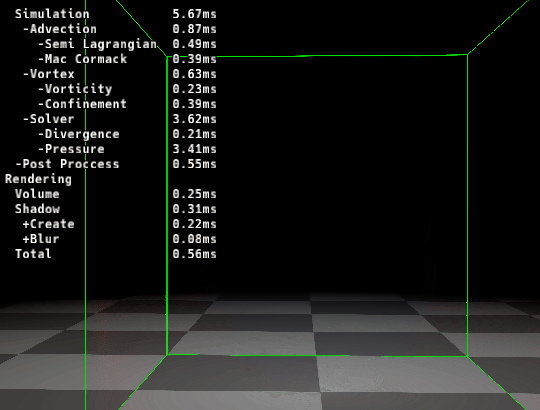▲ 左: マージ前	▲ 右: マージ後

カーネルをマージする事で速度が速くなっていることが確認できます。

3. 圧力ソルバの最適化

流体シミュレーションにおいて、計算時間の 60%〜80% を占めるのが、Projectionステップにおけるポアソン方程式の求解です。

$\nabla^2 p = \nabla \cdot \mathbf{u}^*$

この連立一次方程式をいかに速く解くかが、最適化の最大の山場です。

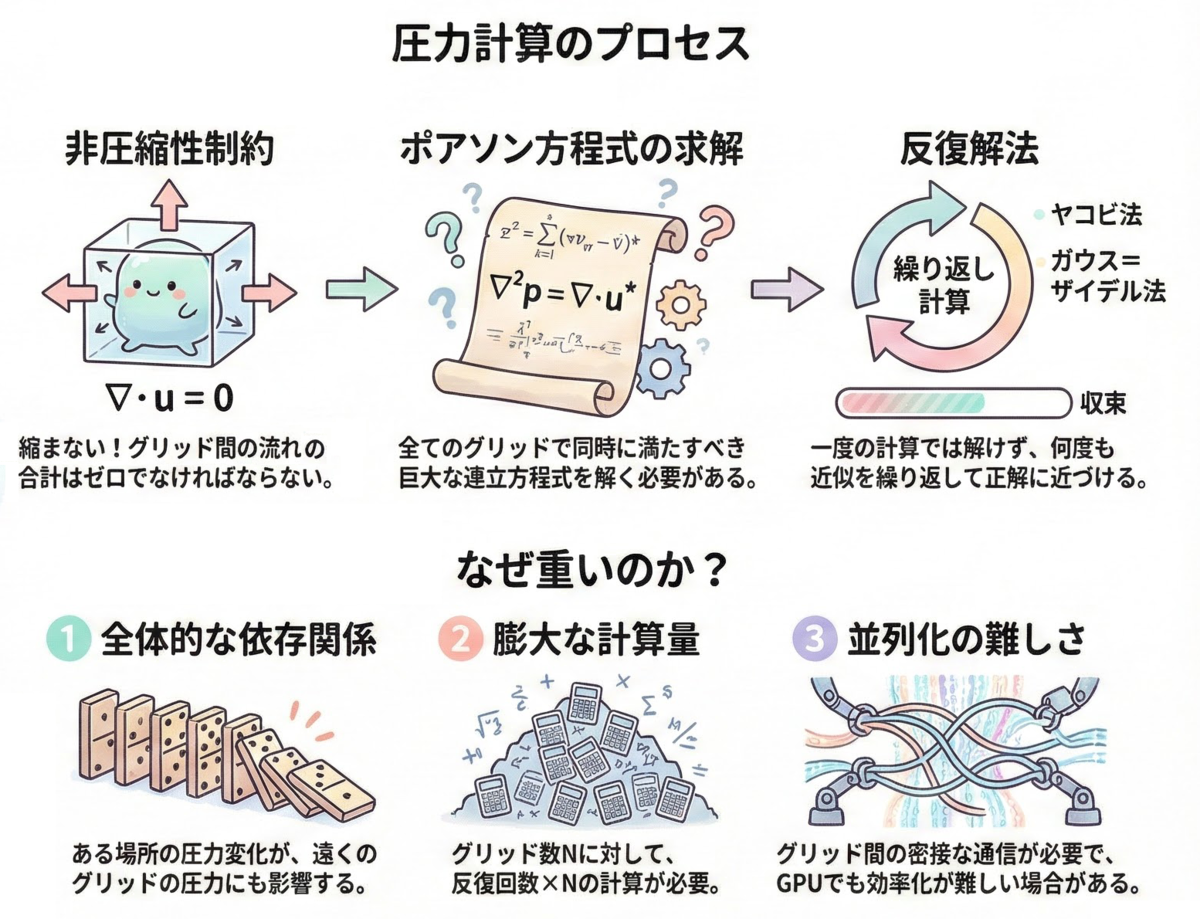
具体的に反復が足りない場合どのような事が起こるかを見てみましょう。


▲ 反復回数少	▲ 反復回数多

反復回数が足りないと圧力が全体に伝わり切らず、爆発のような巨大な圧力が発生したさいに発散してしまいます。

Lv.1 RBGS法（Red-Black Gauss-Seidel）

連立方程式の解法には反復法（Jacobi法やGauss-Seidel法）が用いられます。
しかし、通常のJacobi法などをGPUで実装する場合、読み込み用と書き込み用の2枚のバッファを交互に入れ替える「ピンポンバッファ（Ping-Pong Buffer）」が必須となります。
これはVRAM容量を圧迫するだけでなく、読み書きの切り替えによるオーバーヘッドも無視できません。

そこで採用するのが Red-Black Gauss-Seidel (RBGS) 法です。
グリッドをチェス盤のように「赤」と「黒」のグループに分けます。

Red Kernel: 黒セルの値（固定）を使って、赤セルの値を更新。  
Black Kernel: 更新された赤セルの値を使って、黒セルの値を更新。

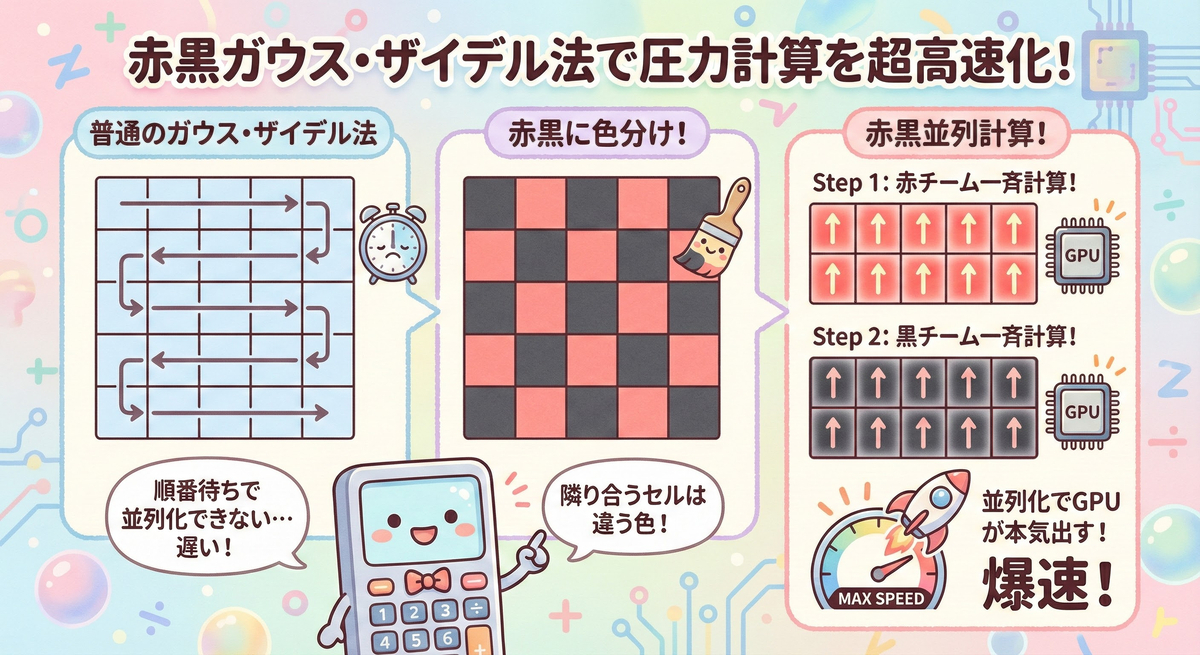
▲ チェス盤パターンによる並列化

この手法の最大の利点は、並列化できることだけではありません。
「赤の更新時は黒を参照するだけ（書き換えない）」という依存関係の明確さにより、1枚のバッファで計算を完結させることが可能になります。

これにより、本来必要だったVRAM容量を半分に削減できるほか、メモリアクセスの局所性が高まることでキャッシュヒット率が向上し、帯域幅の消費も大幅に抑えることができます。
大規模シミュレーションにおいて、この「バッファ1枚」の効果は絶大です。

これにより、依存関係を断ち切り、GPUの並列性能をフルに活かしたGauss-Seidel法が可能になります。

Lv.2 SOR法（Successive Over-Relaxation）

さらに収束を早めるために、SOR法を導入します。

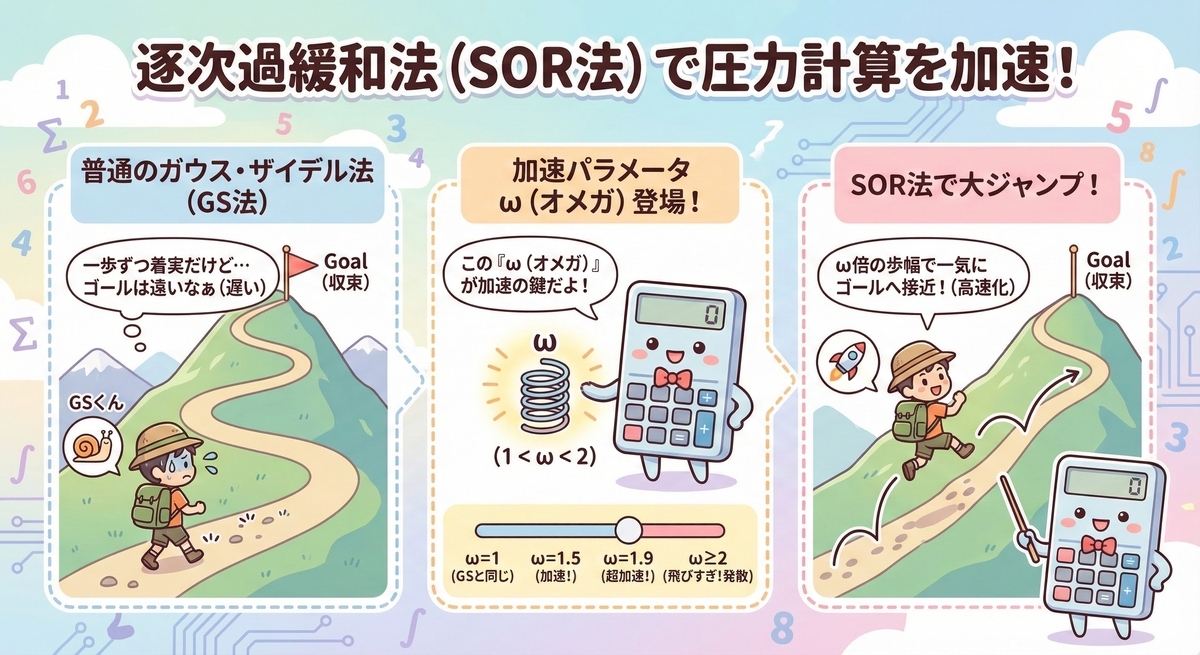
これは、計算された修正量をそのまま適用するのではなく、「少し多めに」修正することで、解への到達を早める手法です。

$p^{new} = (1 - \omega)p^{old} + \omega p^{gs}$

ここで $p^{gs}$ はGauss-Seidelで求めた予測値、 $\omega$ は緩和係数です。
適切な $\omega$ （例：1.8〜1.9付近）を設定することで、同じ反復回数でも残差を劇的に減らすことができます。

コード実装例

void UpdatePressure(uint3 id, int offsetCheck)
{
    // チェッカーボードパターンの判定
    // (x + y) % 2 が 0 か 1 かで、赤/黒を区別する
    if ((id.x + id.y) % 2 != offsetCheck) return;

    // 境界チェック (端のピクセルは処理しないか、別途境界条件で扱う)
    if (id.x == 0 || id.x >= _Width - 1 || id.y == 0 || id.y >= _Height - 1) return;

    // 周囲のテクセル座標
    uint2 L = uint2(id.x - 1, id.y);
    uint2 R = uint2(id.x + 1, id.y);
    uint2 B = uint2(id.x, id.y - 1);
    uint2 T = uint2(id.x, id.y + 1);

    // データ読み込み
    float pL = _Pressure[L];
    float pR = _Pressure[R];
    float pB = _Pressure[B];
    float pT = _Pressure[T];
    float div = _Divergence[id.xy];
    float pC = _Pressure[id.xy]; // 現在の中心値

    // ガウス・ザイデル推定値
    float pTarget = (pL + pR + pB + pT - div) * 0.25f;

    // SORによる過緩和ブレンド
    float pNew = (1.0f - _Omega) * pC + _Omega * pTarget;

    _Pressure[id.xy] = pNew;
}

Lv.3 マルチグリッド法（Multigrid Method）

RBGSやSORを使っても、グリッドサイズが大きくなると、ある問題に直面します。
「高周波の誤差（局所的なズレ）はすぐに消えるが、低周波の誤差（全体的な圧力の偏り）がなかなか消えない」のです。
これが、大規模シミュレーションで反復回数が爆発的に増える原因です。

これを解決するのがマルチグリッド法です。

「細かいグリッドで消えにくい低周波誤差も、粗いグリッドで見れば高周波誤差に見える」という特性を利用します。

V-Cycleの実装フロー

1.Pre-Smoothing: 現在の解像度で数回RBGSを実行。  
2.Restriction: 残差（Residual）を計算し、半分の解像度のグリッドへダウンサンプリング。  
3.Recursive: 最下層になるまで 1〜2 を繰り返す。  
4.Solve Coarse: 最下層で正確な解を求める（反復回数を多めにする）。  
5.Prolongation: 粗いグリッドの補正値を、上の解像度へアップサンプリングして加算。  
6.Post-Smoothing: 再度RBGSを実行して馴染ませる。

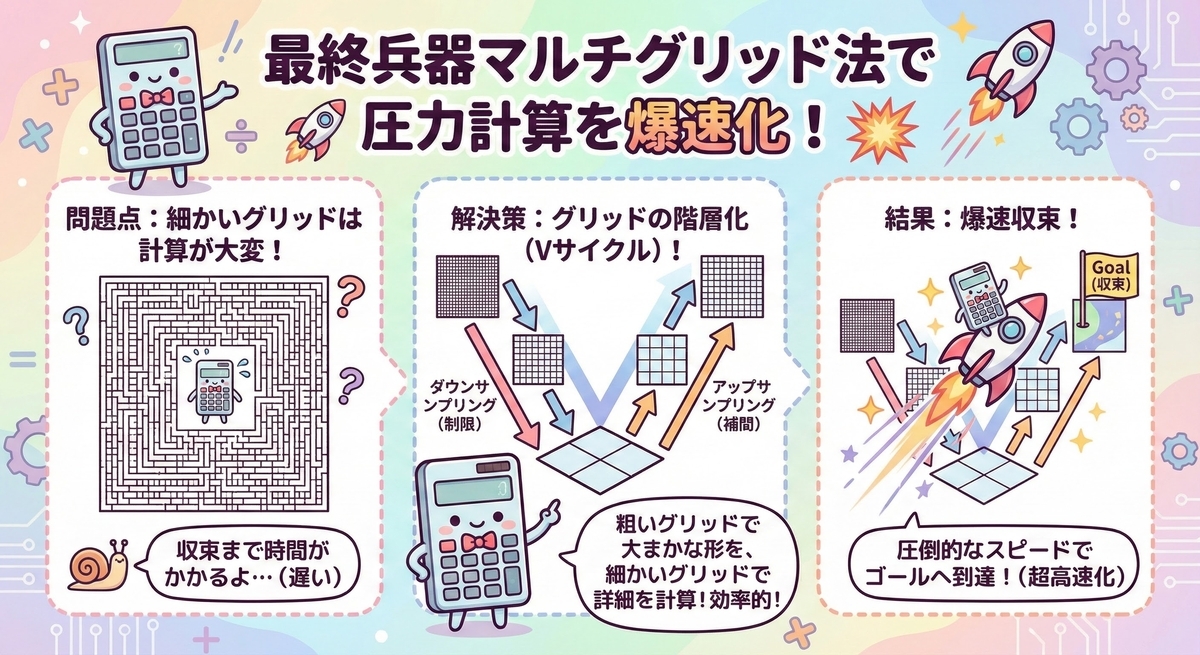
▲ V-Cycleの概念図

驚異のパフォーマンス


▲ RBGS/SOR法	▲ マルチグリッド法

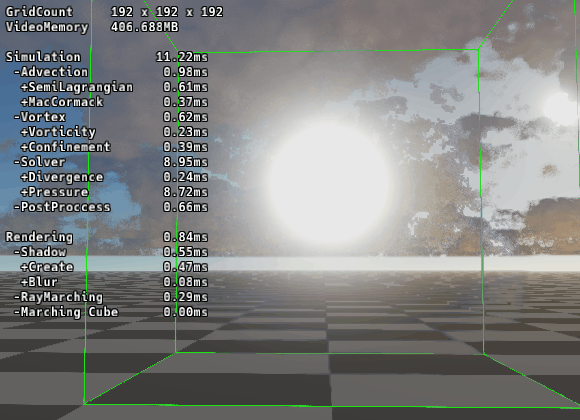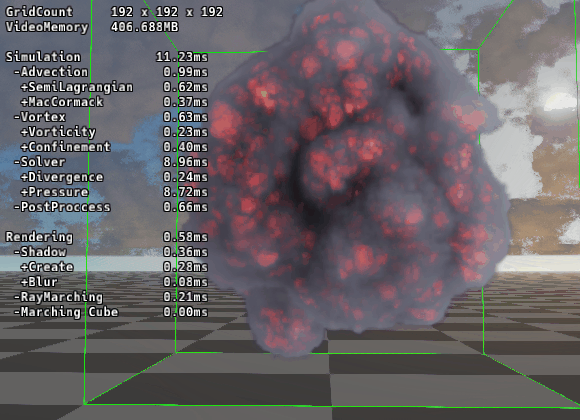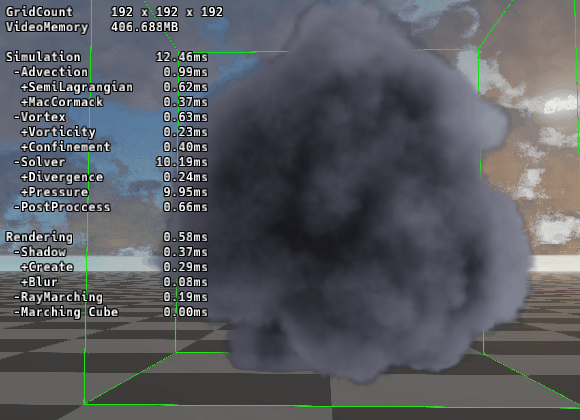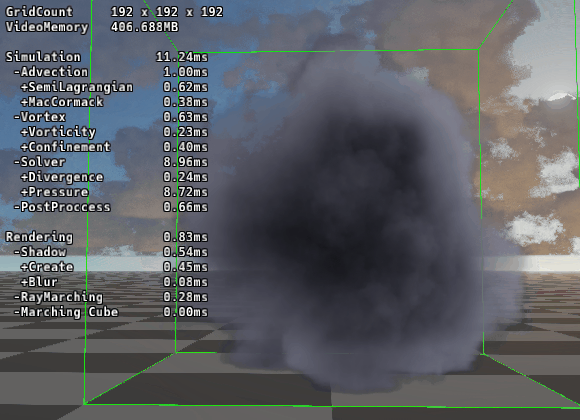
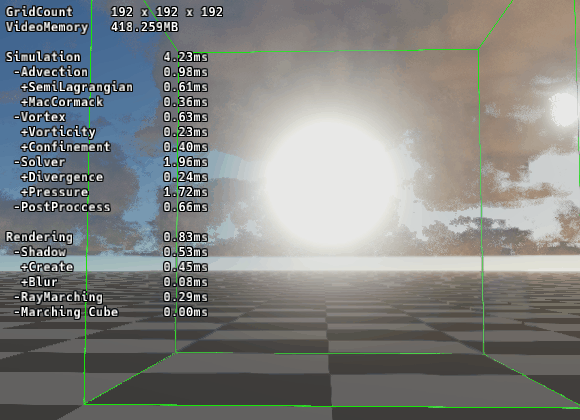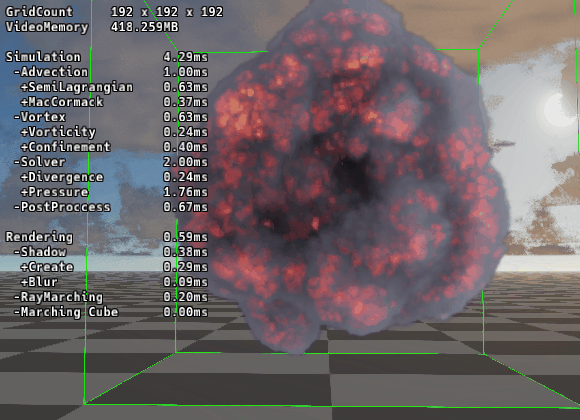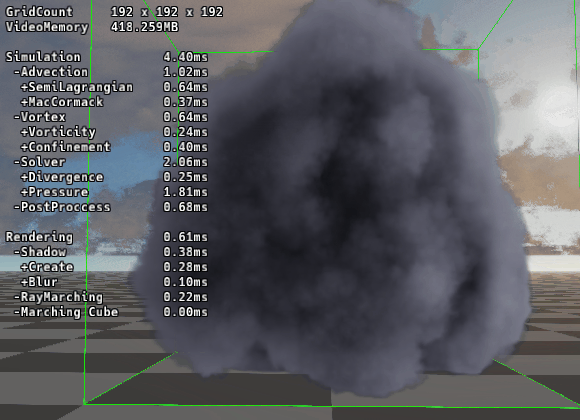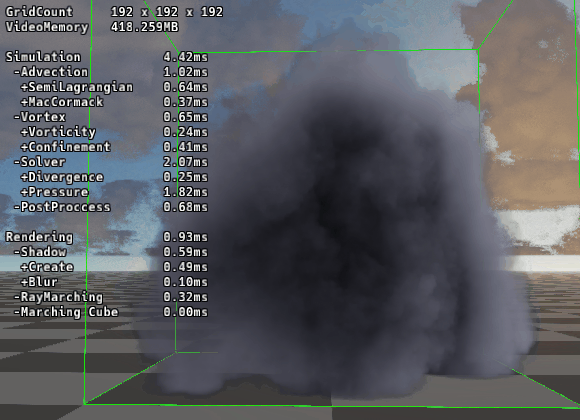
192グリッドでの圧力計算時間を比較しました。

RBGS/SOR法 (24反復): 9.95ms  
Multigrid法 (V-Cycle): 1.81ms

計算手順はかなり複雑になりますが、圧倒的に高速になります。
通常の圧力計算が、グリッド解像度に対して指数関数的に増えていくのに対して、マルチグリッド法は線形にしか増えていかない点も素晴らしいです。
これにより、高解像度でありながらリアルタイムな速度での爆発シミュレーションが現実的になりました。

まとめ

今回の最適化編では、以下の技術を紹介しました。

FP16化: メモリ帯域と容量の節約  
低解像度遮蔽マップ: ソフトシャドウの特性を利用した間引き  
Kernel Fusion: VRAMアクセス回数の削減  
RBGS & SOR: 並列化と収束加速  
Multigrid: 圧力ソルバの抜本的最適化

「物理的に正しい」ことと「計算機的に速い」ことは往々にしてトレードオフの関係にありますが、マルチグリッド法のように数学的な工夫で両立させる事も出来ます。

SPARK GEARではこれらに加えて他にも細かい最適化がされていますが、すべてを書ききるのは大変なので代表的な部分のみを取り上げました。

今回作成した流体のシステムはUnityで動かすことも可能です。
今回は書ききれてないですが流体へのライティングやキャラクターとの衝突判定などの対応も出来ています。
もしUnityでのリアルタイム流体演出をしたいなどのご要望があれば弊社までご連絡ください。

SPARK CREATIVE Tech Blog

https://spark-group.jp/